Mergesort Investigation 3 - recursive implementation
I wrote a traditional, top-down, recursive merge sort. The idea was to see if a different implementation exhibited the same dramatic, abrupt slowdowns. If the different implementation showed the same jumps in timings, the problem is with the operating system, the language run time, or the memory hardware. I know I said I’d ruled out the underlying operating system previously, but I was still suspicious.
The traditional, recursive merge sort did not exhibit the abrupt slowdowns. I think this is a clue that merging power-of-2-length sublists is the cause of the abrupt performance drops.
Traditional, recursive linked list benchmarks
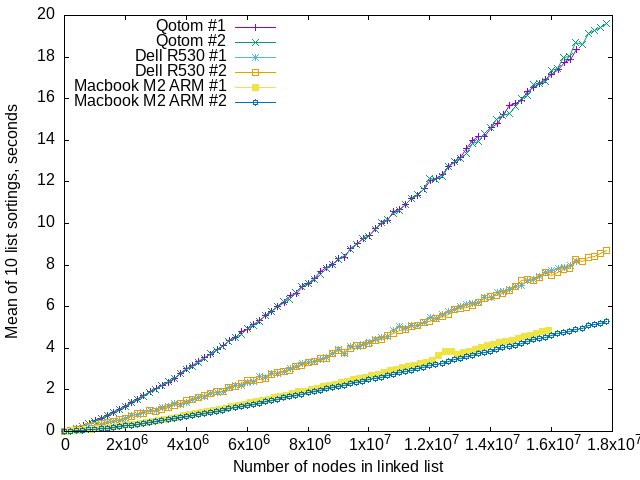
That’s two runs of my benchmark program, on each of three different machines. Each point is the arithmetic mean of timing sorting a randomly-valued linked list 10 times. None of the runs exhibits anything like the abrupt slowdowns my iterative, constant-space algorithm exhibits. Let me emphasize how consistent those runs are on each machine, even on the Dell R530 PowerEdge, which shows the most variation when benchmarking other algorithms.
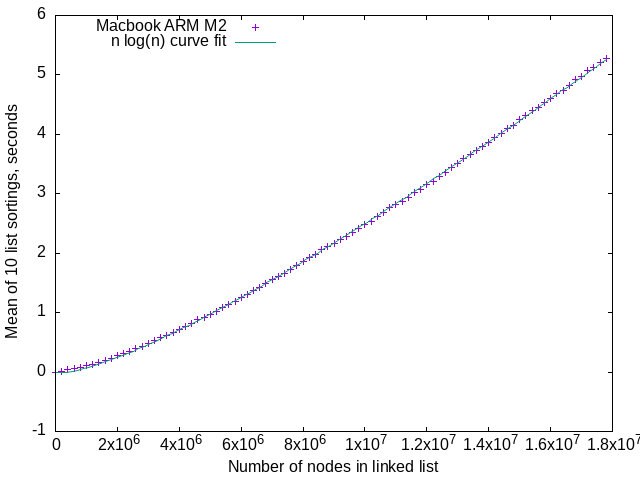
Above, a curve fit of n log(n) to the actual performance,
the “Macbook M2 ARM #2” points on the graph one more up.
I used gnuplot to do the curve fitting,
The n log(n) curve is:
a = 7.93461e-08
b = 2.33542e-06
g(x) = a*x*log(b*x)
Could not be a better fit. This satisfies me that a recursive, top-down merge sort is O(n log(n)) in time complexity.
This version of mergesort was substantially easier to write and get correct than the one I wrote to solve a Daily Coding Problem in July 2021. I speculate that the “constant space” requirement on the original problem existed to keep candidates from writing a recursive version.
