Count number of heaps coding problem

Another programming interview question from the Daily Coding Problem email list. I received it as #1608.

Daily Coding Problem: Problem #1608 [Medium]

This problem was asked by Microsoft.

Write a program to determine how many distinct ways there are to create a max heap from a list of N given integers.

For example, if N = 3, and our integers are [1, 2, 3], there are two ways, shown below.

  3      3
 / \    / \
1   2  2   1

Repo for my code.

A heap is a data structure, By “data structure” I mean an organization, management, or storage format that is chosen for efficient access to data.

Heaps are usually understood as binary trees. Each node has a sortable value, and at most 2 child nodes. The nodes are arranged so that every node’s value is greater than either child node’s value. Note that the values aren’t strictly sorted like in a Binary search tree, they’re only partially ordered. The node with the largest (or smallest) value is the root node, which is the efficient access to data part of a data structure.

The binary tree also has a specific “shape”. Every interior node has 2 children except for the bottom row, which is filled in left-to-right. Here’s an example:

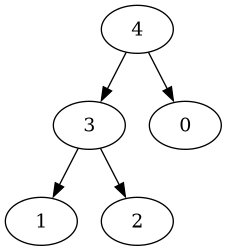
Even though all nodes have values greater than those of their child nodes, I find the layout unintuitive.

Despite the odd criteria, which mean that the “ordering” of the node’s values is not very easy to envision, heaps occur all over the place because they can be used to keep track of things that have to occur in an order. Putting in new events or data items is quite fast because the ordering is a little sloppy. A program doesn’t have to do as much calculation. Heaps can also be used to sort items quickly.

Because of the weird layout possibilities, I could not figure out a clever way to count layouts of heaps without just checking candidates. It turns out there is a way to count heaps, if each of the integer values is unique, but it’s obscure and difficult. If you read the problem statement closely, you won’t see “list of unique integers”.

Binary tree as a variable-length array

It turns out that one way of keeping track of a binary tree is in an array, a row of data values accessible by a numerical index.

The children of the node at index n would have indices 2n + 1 and 2n + 2 in a zero-based array. For zero-based arrays (which is the One True Way to index), the parent of the node at index n is located at position (n-1)/2 (floored). The “floored” part means that any fractional remainder is ignored: 5/3 (floored) is just 1 This is a super-convenient way to store a heap-structured binary tree, because preserving the “shape” is just appending any new data items to the end of the array. Keeping the partial ordering property, with the largest (or smallest) value node at the root is only a little more complicated, and doesn’t end up mattering to solving this problem.

It is possible to examine the array to decide if, as a heap, the nodes are partially ordered. That’s the key to my solution: generate all permutations of the integers in the list of N integer, then inspect the arrays containing those permutations for the heap partial order property.

Permuting an array

Confusingly, a fellow named “B. R. Heap” invented or discovered an algorithm for generating all permutations of values in an array. My solution uses Heap’s algorithm to generate permutations, which get examined for the partial ordering property.

Heap’s Algorithm is recursive, so it fits into a Go language pattern of generating answers or potential answers in one thread of control, then counting or picking unique answers or outputting in a second thread of control. For recursive answer generation, this makes the code a lot clearer. The recursive function’s signature does not contain a number of arguments that only get used when recursion terminates. The recursive function does not contain much code to decide if a particular putative solution actually constitutes a solution.

Possible heaps for 4 unique values

Here’s what my program finds as the 4 possible heap layouts for the list of integers 0, 1, 2, 3, 4:

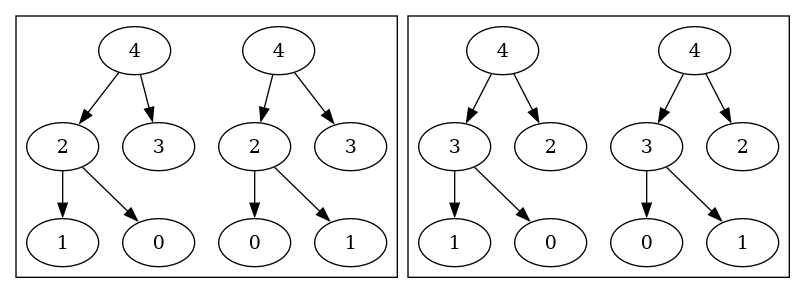
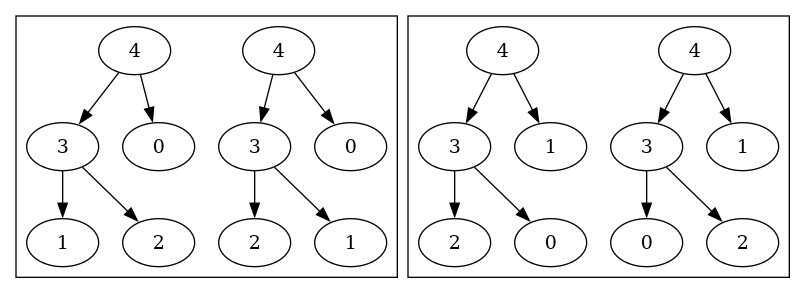
You can see that pairs of values get swapped to make different heaps.

None of these partial orderings makes up a totally ordered binary search tree. In fact the only binary search trees that are also heaps are two element trees, where the max value is the root, and the lesser value is the root’s left child.

Recursive Count Calculation

There is a way to count heaps, if each of the integer values is unique,

I wrote a program that does this calculation. Whoever worked this one out is an absolute genius.

What was Microsoft thinking?

This is not a good interview question.

Did they want someone to remember (or derive on the spot) the recurrence relationship above, and then write a program implementing that calculation? Writing that program is full of pitfalls. The “combinations of n-1 items taken b+r₂ at a time” part invites integer overflows unless done carefully. I cheated and used the Gamma function, which works in floating point arithmetic. I converted the floating point combinations answer back to an integer. There’s two places to do “floor” operations, a log-base-2 and an integer division that could cause problems.

Did they want people to do what I did, generate heaps and weed out non-unique answers, so they could see some programming skill? That seems like a lot for an whiteboard interview question. I personally find that Heap’s Algorithm is entirely inobvious. The only reason I could use it was because I knew the trick about representing binary trees with a variable length array. If a candidate went with a binary tree representation that explicitly referenced child nodes, generating permutations would involve building binary trees by inserting values in different orders. Something like this would give a candidate opportunities to demonstrate coding ability, but would take a lot of time.

Is it about algorithms? A mid-career programmer can be assumed to have heard of a heap, but mainly in the context of prioritizing tasks. Heaps are sometimes known as “priority queues”, but nobody is going to remember the details of implementation. Someone who has just taken an algorithms and data structures class might recall details of heaps, and that permutation algorithms exist.

I’m not so sure my solution is any good, but the way the question is phrased, the candidate can’t assume a list of N unique integers. Maybe I’m over-thinking this problem, but anyone who has done some professional software development will be on the lookout for restrictions (or lack of restrictions) on inputs due to having gotten burned by not noticing some trivial phrase or word in the requirements, and assuming too much or too little.