Binary Tree Package Design
Source code for my Golang binary tree package.
I’m not going to elaborate on the nature of binary trees: there’s plenty of tutorials and educational material that cover binary trees. I’m just going to write about my particular implementation, and my opinions about why that implementation works well.
History
I’m interested in what it’s possible to calculate, so I often get diverted into doing little programming puzzles. A lot of those puzzles deal with either linked lists or binary trees, and sometimes both, like the Great Tree-List Recursion Problem.
Over the years, I’ve done many binary tree programming puzzles.
I’ve done them in various programming languages, in the past C, for the last few years, Go.
I subscribed to the Daily Coding Problem email list a few years ago.
I did a few Daily Coding Problem binary tree problems,
then realized that I was writing redundant code.
I fixed bugs in some problems’ code but not others
because I didn’t have a centralized binary tree library.
Ultimately, I combined the problems I had already completed
into a single Git repository,
and made a binary tree Golang package,
imaginatively named tree.
The evolution of that package went something like this:
- Numeric-valued nodes (
type Node struct) with un-exported data and child pointers. This meant that all problems’ code ended up in the package. - GraphViz tree representation output, for numeric-valued nodes only.
- Implementation of string-valued nodes (
type StringNode struct) with exported data and child pointers. Some problems don’t use numbers as the data in nodes, and they want you to start with unordered trees, or trees with very specific “shape”. - Change GraphViz output-generator to internally
use
type drawableinstead of*Node, which was the numeric-valued node type at the time.type drawablehadLeft() drawable,Right() drawableandIsNil() boolmethods, presagingtype Node interface.- Also, numeric- and string-valued nodes with exported data and child pointers.
- Write generalized traversal functions to use
Nodeinterface and function pointers that can be called pre-, post- and in-order. I generalized the traversal functions by allowing the user to put in per-visited-node function pointers, not generalized in the sense of “can handle both tree node types”. - Rework generalized traversal functions to use
type drawable interface. Note thatdrawableisn’t exported, so users of packagetreecan’t write generalized functions on trees. Now the traversal is handled by common code, and that common code can traverse trees with both types of nodes. - Change numeric-valued
type Node structtotype NumericNode struct. Merely renaming, but a step none-the-less. - Add command line string representation of string-valued-node trees as a Lisp-like parenthesized string.
- Generalize string-value and numeric-value nodes with a Golang
type Node interface. Convert a few functions to useNode interfacerather than*StringNodeor*NumericNode, most notably the GraphViz tree representation output. Add aString() stringmethod totype Node interfaceas part of this. - Rewrite the tree-as-parenthesized-string parser of item (4) above using the generalized traversal functions.
Have a
*NumericNodeand a*StringNodeversion, because some problems want one or the other.
Note that I say the package “evolved”.
I changed things as I learned,
or encountered a coding problem that demanded more flexibility.
Some earlier problems (like “invert a binary tree”) ended up in the package code
because I hadn’t exported tree-node struct elements.
I ended up writing second and sometimes third or fourth version of code solving some problems
because I wanted to see if the generalized Node interface would work well.
I think that changing code as you learn may be the only way to get to sleek, usable library code. I don’t think that spending huge amounts of time on design and architecture up front will entail a good library package. Even the wise do not see all ends.
What makes this package interesting:
- Both string- and numeric-valued nodes fulfill a generalized Node interface. The Go programming language makes this possible.
- The “tree” type is merely the tree node type
- Use functions on tree structures, methods only act on individual items.
- Check for nil pointers at the beginning of recursive functions acting on trees.
Checking for nil “object” pointers on methods is allowed by Go,
and methods in
treeacting on instances oftype *NumericNodeortype *StringNodealso check at their beginning. - Generalized traverse functions.
- GraphViz output of entire trees, generalized over both value-types of nodes.
Some of these derive from binary tree programming puzzles, some derive from software engineering (via gradual code evolution), some exist because the generalized node interface exists. Go allows methods to act on nil-valued pointers, enabling a technique to increase code clarity.
interface Node
Making a Go interface that covers both *StringNode and *NumericNode
would seem like the first step on the journey.
As the timeline above shows, type Node interface evolved from a type drawable interface
that wasn’t exported from package tree.
It was close to the last step in the journey.
type Node interface {
LeftChild() Node
RightChild() Node
SetLeftChild(Node)
SetRightChild(Node)
IsNil() bool
String() string
}
This interface does mandate “getters” and “setters” for child nodes.
I’m not sure that particular OOP doctrine applies to Go interfaces.
My original generalization, type drawable interface in package tree
did not have SetLeftChild() and SetRightChild() methods,
because drawable was used only with already complete and existing trees:
it was never used to create a new tree.
Lots of functions operate on interface Node,
and thus work on trees of both string- and numeric-valued nodes
The alternative might be a node type that allows any data value type:
// hypothetical alternative generalized tree node
type GeneralizedDataNode struct {
Data interface{} // or any
Left *GeneralizedDataNode
Right *GeneralizedDataNode
}
The price of this is doing type assertions for tree operations like ordered insert to produce Binary Search Trees, and maybe special functions for insertion of each data value type. One side benefit: you could build trees with mixed string, numeric, or other valued nodes.
A Single Node Type
Each binary tree comprises elements of a single type, *NumericNode or *StringNode,
with no special tree type that contains the root data node.
My package makes no compiler-type-level distinction between “leaf” and “interior” node.
There is no type or interface InteriorNode or LeafNode.
There’s no benefit in having a type-distinction between an interior and a leaf node,
unless you rely on an object oriented virtual method scheme to
do things like terminate recursion, pick which child to recurse on, etc etc.
Since I cleave to the doctrine that functions act on structure,
while methods act on data,
I have functions doing recursion.
I think this is the right decision,
because recursion ends up having to check at least one pointer for nil anyway.
You can’t do a node.Left.(LeafNode) type assertion without checking for nil first.
It just doesn’t pay off to have special leaf node types.
Creating binary trees
A “tree” as an instance of *StringNode or *NumericNode,
not a special tree type,
simplifies functions dealing with trees.
For example, inserting a node into an ordered tree ends up looking like this:
var root *tree.NumericNode
root = tree.Insert(root, value)
Since tree.Insert() has to check for a nil node argument,
it can handle all node allocations,
including for the root node.
No special case coding needed.
This ends up looking like a “functional programming” data structure.
Having a “tree” type, different from a “node” type,
that “HasA” root node element would entail allocating the “tree” type first,
then setting the root node.
Functions which accept a tree would extract the actual data node root,
and have a helper function do the actual work.
A binary tree as type *NumericNode minimizes boilerplate all around.
Functions, Not Methods
Methods should act on object’s internal data.
Therefore, this package has functions that deal with the tree structure itself,
not object oriented methods.
The methods would end up duplicating code
in each type Node implementation
to do things like terminate recursion,
or they’d just be forms of the rightly-scorned “getters” and “setters”.
The correct place to test for
nil pointers is at the beginning of a recursive functions,
like tree.Insert or tree.BstProperty.
That is, take the penalty for an extra function call on nil child pointers.
This avoids redundant code checking on nil left- and right-child pointers.
It reduces visual clutter, promoting easy understanding.
Recursion obviously bottoms out in a single place,
promoting program correctness.
In the insert case, it also allows your code to create nodes in a single, sensible, place.
Generalized traversal function
It’s possible to write and use a generalized tree traversal function:
type VisitorFunc func(node Node)
func AllorderTraverseVisit(node Node, preorderfn, inorderfn, postorderfn VisitorFunc) {
if node.IsNil() {
return
}
if preorderfn != nil {
preorderfn(node)
}
AllorderTraverseVisit(node.LeftChild(), preorderfn, inorderfn, postorderfn)
if inorderfn != nil {
inorderfn(node)
}
AllorderTraverseVisit(node.RightChild(), preorderfn, inorderfn, postorderfn)
if postorderfn != nil {
postorderfn(node)
}
}
Creating GraphViz output
GraphViz is one of the most useful pieces of free software.
Writing just a few lines of text input allows creation of nifty images like this:
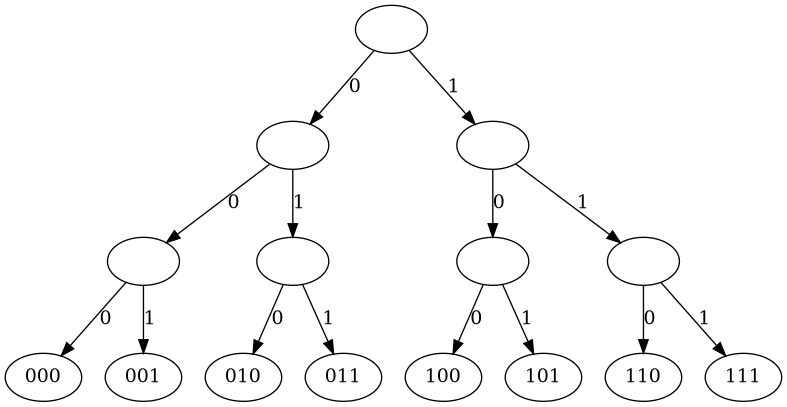
My binary tree package has a 46-line file which contains functions that work on both string- and numeric-valued trees, and can produce GraphViz input for graphical representations of binary trees.
Reading in a tree
I wrote a function to parse a Lisp-like, parenthesized string, turning it into a binary tree.
A string like this:
(root (left (leftleft) (leftright)) (right () (rightright)))
into a tree that can be drawn like this:
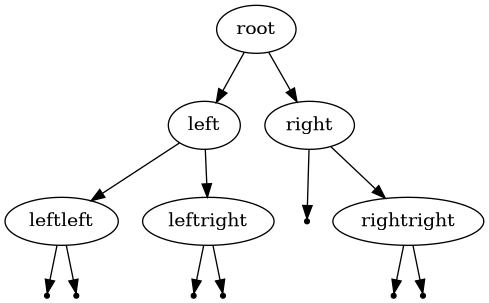
I’ve found this immensely helpful in debugging some of the puzzles’ code.
Drawing trees like this motivated my generalization of the tree node type. It’s not something that occurred to me in advance.
Binary Tree Uses
Outside of binary tree programming puzzles that this package facilitates, binary trees get used in a lot of programs. A few programs I’ve written that rely on binary trees as their core data structure:
In all three (2 in Go, 1 in C) of these programs, binary trees constitute the in-memory representation of some structure: numbers and operators (+, -, % etc), propositional logic variables and connectives, combinatory logic primitives and the application operation. Unlike in this binary tree package, only leaf nodes have a value per se, interior nodes represent some logical or arithmetic operation to be performed.
