Across the Space Frontier - circumlunar trip

Across the Space Frontier, Joseph Kaplan, Wernher von Braun, Heinz Haber, Willy Ley, Oscar Schatchter, Fred Whipple, edited by Cornelius Ryan, Viking Press, 1952. part of a prose exposition and elaboration of von Braun’s The Mars Project, the technical appendix of Project Mars,

Von Braun describes a lunar excursion, to be undertaken as a way to ease into interplanetary travel, and map the landing site for a lunar expedition.

Above, the lunar probe flying 50 miles above the moon’s surface. Astronauts are maneuvering a large reflector telescope camera to get close-up pictures of the surface.

Here’s von Braun’s own sketch, which actually gives a scale:

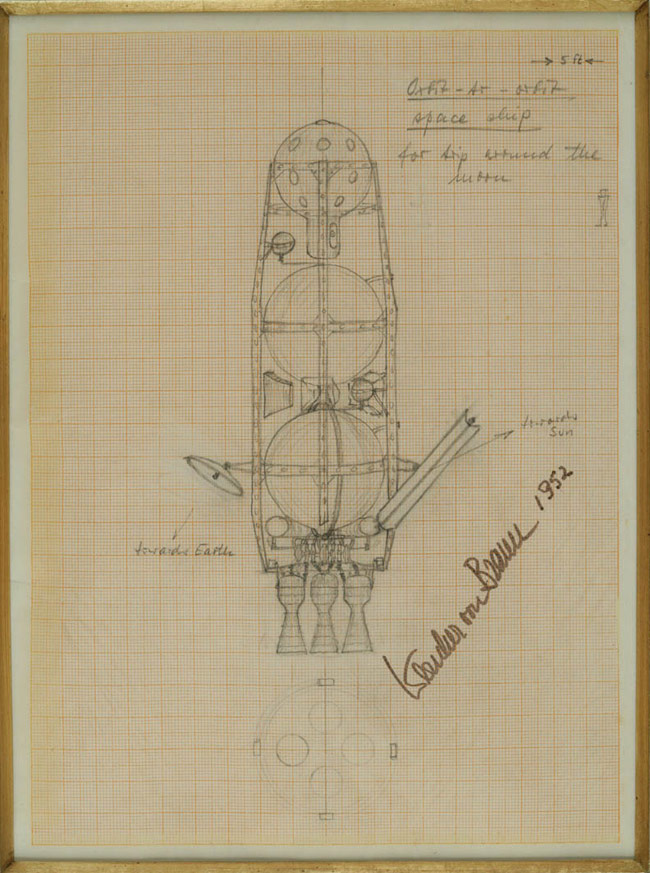
The line drawings in Across the Space Frontier are based on von Braun’s sketches!

“The propulsion unit is the same as that of the Third Stage”.

The PRINCIPAL DATA ON THE THREE STAGE ROCKET SHIP table has these relevant facts for the Third Stage:

• 220 ton thrust
• 0.77 ton/sec propellant consumption
• 9200 ft/sec exhaust velocity
• 286 sec I_sp

There’s a phrase that leaving space station orbit requires “barely 2 minutes” of thrust.

Convert to consistent, sensible, units

ΔM = (120 s)(0.77 ton/s)(2000 lb/ton)(1 kg/2.2 lb) = 84000 kg

That’s for a single 120 second burn.

ΔV = 6340 mi/hr * 5280 ft/mi * 1/3.28 m/ft * 1/3600 hr/sec = 2835 m/s

Thrust = 220 ton * 2000 lb/ton * 4.45 N/lb = 1.958E6 Kg m/s²

V_exhaust = 9200 ft/sec * 1 m/3.28 ft = 2805 m/s

Use Rocket Equation to back out the starting mass of vehicle

The vehicle has to do twice the 2835 m/s ΔV, once to leave for the moon, and once to re-circularize its orbit with the space station.

ΔV = V_exhaust ln(M₀/M_f)

2*2835 m/s = (2805 m/s) ln(M₀/(M₀ - 2*84000 kg))

ln(M₀/(M₀ - 2*84000 kg)) = 2.022

M₀/(M₀ - 2*84000 kg) = 7.549

M₀ = 7.549M₀ - 1268232 kg

6.549M₀ = 1268232 kg

M₀ = 193652 kg, the fully fueled mass of the vehicle

Dry mass is about 196,652 - 2*84000 = 25652 kg, or 28 US tons.

Double check M₀ result

The PRINCIPAL DATA ON THE THREE STAGE ROCKET SHIP table has the Third Stage, the re-entry vehicle whose propulsion unit this vehicle re-uses, as 143 tons. Without wings, very light structure and spherical fuel tanks, the circum-lunar vehicle at 28 US tons is pretty darn light.

The scale on von Braun’s sketch puts the diameter of fuel and oxidizer tanks at 20 ft = 6.0 m, for a volume of 113 m³

Assuming 100% full tanks (which may be incorrect), and noting that hydrazine has a density of 1.021 g/cm³, total mass of hydrazine for a full tank is 115,300 kg

Commercial grade fuming nitric acid has a density of 1.50 g/cm³, 168,500 kg total mass for a full tank.

The tanks can hold 2*84000 = 168,000 kg of propellant.

Looking at N₂O₄ and Aerozine-50 engines like the Aerojet LR87, we see a fuel:oxidizer ratio of 1.9. I interpret that to mean that 1.9 kg of hydrazine combusts with 1 kg of N₂O₄. 168,000 kg of propellant would mean (1.9/2.9)*168,000 = 110,070 kg of hydrazine would get used, which is really close to the 115,300 kg full tank calculated above. The N₂O₄ tank would only have (1/2.9)*168,000 = 57,930 kg, about a third full.

The mass ratio of the ship is 196652/25652 = 7.67

Real life LR87 engines ended up with an I_sp of 302 seconds when development was complete, as opposed to the 286 second specific impulse assumed in my calculations and simulations. Von Braun’s 3-stage launch vehicles would encourage lots of development of the engines.

The Orbit Diagram

This is the orbit as presented in Across the Space Frontier. This diagram presents the vehicle’s trans-lunar orbit in the same plane as the space station’s orbit and the moon’s orbit. Earlier in the book, von Braun and his co-authors go well out of their way to describe the space station’s orbit, and it’s not equatorial, but rather perpendicular to the plane of the moon’s orbit.

Double check by simulating vehicle’s orbital mechanics

I took an orbital mechanics class in 1982 or 1983. That was a long time ago. My celestial mechanics are rusty. As a means of double checking this vehicle, and at the same time re-learning some orbital mechanics, I wrote a numerical simulation of this vehicle. The simulation is simple, a 2-D Euler’s Method numerical integration. I did not include the complicating effects of lunar gravity. I did do Symplectic integration, which generally works better than “naive” Euler’s Method integration, but that really was a matter of luck.

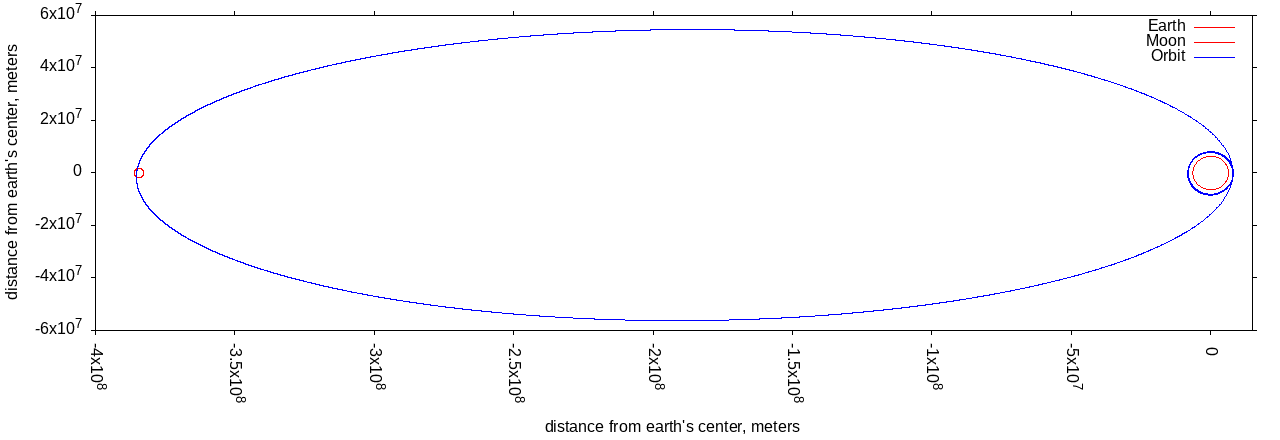
Above is a to-scale diagram of the earth, a 1075 mile high space station orbit, and the elliptical trans-lunar orbit. There are to-scale red circles for the earth and moon, but I did not include the effect of lunar gravity. The red circles appear to visually verify that the orbit gets out to the moon and back.

Circularizing the orbit after coming back from the moon leaves the vehicle with a mass of 27402 kg, leaving just 1750 kg of propellant. Such a vehicle would have required careful engineering, with an emphasis on saving mass. My simulation predicts a maximum acceleration of about 7.3g. I think throttling the engines would allow lower accelerations (and loads), but that would use more propellant.

My simulations strike me as indicating this vehicle and flight plan are just barely possible.

The only way I can understand the orbit diagram from Across the Space Frontier is to have the plane of the page be the plane of the space station’s orbit, with the moon’s orbit perpendicular. The artist could have done a better job indicating that the moon’s orbit is normal to the vehicle’s orbit, if that’s true.

Code repo for the simulations.

In Fiction

Lester Del Rey included a fictional account of a circum-lunar excursion apparently modeled after von Braun’s in Mission to the Moon. His hero, young Jim Stanley, gets selected to pilot the lunar probe.

In Real Life

Apollo 8, the high point of western civilization, was the first human mission to leave earth orbit, fly to the moon and return. It did not leave from an earth orbiting space station, but rather depended on higher efficiency propellants than von Braun assumed, and had maybe 5 stages depending on how you count them.

Apollo 8’s trans-lunar injection has the S-IVB stage burning for about 350 seconds, for a ΔV of 3.05 to 3.25 km/s. That’s somewhat more than the 172 second, 2.7 km/s ΔV my simulation did.

There were lots of differences from von Braun’s fly by proposal. Apollo 8 didn’t do a large eccentricity elliptical orbit. NASA put it into a more complicated free return trajectory. Apollo 8 did not return to earth orbit. The crew capsule scrubbed off the ΔV by directly entering the earth’s atmosphere.

A polystyrene kit of this orbiter got some legs tacked on and marketed as a Mars lander, or a lunar lander.

Grant Hutchison assembled this kit without the landing legs and other mods to make the kit more like von Braun’s conception.

A custom build model that’s far truer to von Braun’s design.